Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- pccp기출문제
- c++
- 정렬
- 알고리즘 문제풀이
- div2개
- 알고리즘문제풀이
- 스택
- Lv2
- 과제진행하기
- solved.ac골드
- React.StrictMode
- 백준알고리즘
- solved.ac플래티넘
- 두원사이의정수쌍
- 비트마스크
- Lv3
- 지도 여러개
- 2023카카오블라인드코테
- 코어자바스크립트
- JS스터디
- 프로그래머스
- 백준 알고리즘
- [pccp 기출문제]
- 이중지도
- 최소스패닝트리
- JS
- 5강클로저
- DP
- 타겟넘버
- 우박수열정적분
Archives
- Today
- Total
호지
[백준 알고리즘] 2162번 선분 그룹 c++ 본문
역시 알고리즘은 끝이없다
두 선분이 만나는지 여부는 CCW알고리즘을 통해 구할 수 있다
CCW알고리즘은 3점의 방향성을 나타내고
시계방향일때는 -1, 직선일때는 0, 반시계방향일때는 1을 반환한다.
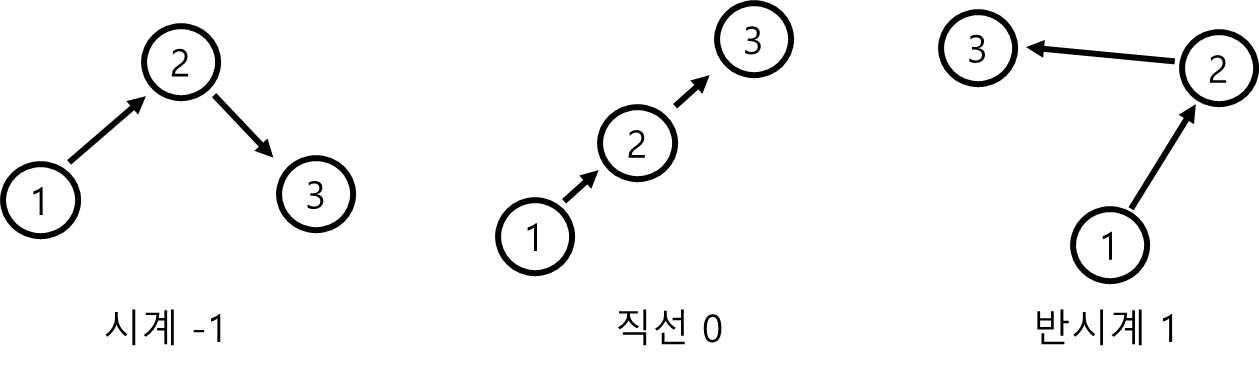
이 방향성을 응용하여 선분이 만나는지 확인할 수 있는데,
선분1 a(x1, y1), b(x2, y2)
선분2 c(x3, y3), d(x4, y4)
이 주어졌을 때
선분ab와 점 c, 선분 ab와 점 d의 ccw값이 둘 다 -1이거나 둘 다 1이면
선분 ab와 선분 cd는 만나지 않는다.
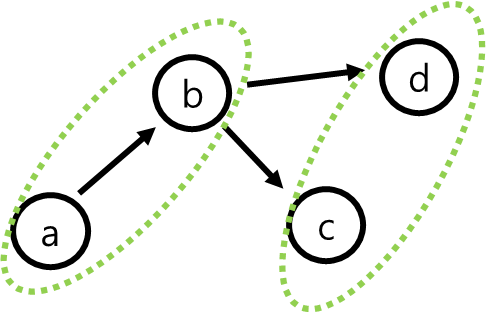
위를 이용해 ccw를 값을 이용해 선분ab, 선분 cd에 대해
교점이 있는지 확인하는 check 함수를 구현했다.
각 점에 대한 ccw값인 abc, abd, cda, cdb를 구하고,
if(abc*abd ==0 && cda*cdb ==0)
를 통해 두 선분이 같거나 평행할 때를 확인한다.
각 선분끼리 check함수를 확인하여
두 선분이 만나면 부모노드를 합치고,
그룹의 수를 저장한 count배열도 합친다.(union_root호출)
최종적으로 count함수에 각각 그룹에 속한 선분이 몇개인지 저장되어 있고,
이를 전체 탐색함으로 선분의 개수가 최대인 그룹과, 총 그룹의 수를 구할 수 있다.
#include <iostream>
using namespace std;
using pp = pair<int,int>;
pp start_point[3001], end_point[3001];
int parent[3001], count[3001];
int ccw(pp a, pp b, pp c){
int tmp = a.first*b.second + b.first*c.second + c.first*a.second - (a.second*b.first + b.second*c.first + c.second*a.first);
if(tmp > 0)
return 1;
if(tmp < 0)
return -1;
else
return 0;
}
bool check(pp a, pp b, pp c, pp d){
int abc = ccw(a,b,c);
int abd = ccw(a,b,d);
int cda = ccw(c,d,a);
int cdb = ccw(c,d,b);
if(abc*abd == 0 && cda*cdb ==0)
return max(a,b) >= min(c,d) && min(a,b) <= max(c,d);
return abc*abd <=0 && cda*cdb <= 0;
}
int find_root(int a){
if(a == parent[a])
return a;
return parent[a] = find_root(parent[a]);
}
void union_root(int a, int b){
a = find_root(a);
b = find_root(b);
if(a!= b){
parent[b] = a;
count[a] += count[b];
count[b] = 0;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int n;
cin >> n;
for(int i=0; i<n; i++){
cin >>start_point[i].first;
cin >>start_point[i].second;
cin >>end_point[i].first;
cin >>end_point[i].second;
parent[i] = i;
count[i] = 1;
}
for(int i=0; i<n; i++){
for(int j=i+1; j<n; j++){
if(check(start_point[i],end_point[i],start_point[j],end_point[j])){
union_root(i,j);
}
}
}
int group_cnt = 0, max_count = 0;
for(int i=0; i<n; i++){
if(count[i] != 0){
group_cnt ++;
max_count = max(max_count, count[i]);
}
}
cout << group_cnt << "\n" << max_count;
return 0;
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준 알고리즘] 2239번 스도쿠 문제풀이 (0) | 2022.06.08 |
|---|---|
| [백준 알고리즘] 2166번 다각형의 면적 (0) | 2022.06.08 |
| [백준 알고리즘] 2143번 두 배열의 합 문제풀이 c++ (0) | 2022.05.07 |
| [백준 알고리즘] 2098번 외판원 순회 c++ (0) | 2022.05.06 |
| [백준 알고리즘] 1987번 알파벳 문제풀이 c++ (0) | 2022.05.05 |
Comments